나의 작은 valley
15) 다변수 미적분학 (하) 본문
스토크스의 정리(Storke's Theorem)
그린정리를 아주 조금 변형하는 것에 지나지 않는다. 폐곡선의 내부를 z축 방향으로 잡아 당긴 형태의 그림을 상상해보자.

새로운 FTC 정리 만들기
1) 주어진 도형의 폐곡면을 N등분한 직사각형들이 그림처럼 위치한다. 각 직사각형들은 크기가 서로 다를 뿐더러 같은 평면 위에 주어지지 않으므로 이 직사각형들을 밑면으로 사용하기 위해서는 각 직육면체의 높이를 새롭게 정해 주어야 한다.
옆면을 단순화하여

이렇게 그리자.
각 직사각형 타일 조각마다 그 접평면에 수직이고 크기가 1인 법선벡터 N을 만든다.
또한 우리는 이 3차원 공간 위에서의 벡터장의 회전량을 알수 있다.(기호로 ∇xF)
∇xF 과 법선벡터 N을 내적하여 값(크기)를 결정지을 수 있다. 이 값을 직육면체의 높이로 사용하자.
이제 높이를 구했으니깐 직육면체의 부피를 더하고 N을 무한대로 바꾸면 껍데기 S 위에서 F의 회전량을 다 더한 의미가 될 것이다. 이를

로 적고 ∇xF의 면적분 (Surface intergral) 이라고 한다.
스토크스의 정리(Storke's Theorem)

그린 정리에 일반화에 지나지 않는다.'
발산 정리 (Divergence Theorem)

스토크스의 정리에서 본 그림에서 내부영역마저 꽉 채워진 완전한 3차원 공간이다.
적분하는 영역은 곡면 s에서 곡면 s의 채워진 내부 v로 확대 되었고
이떄 적분하는 영역(경계면)은 곡면 s이다.
3차원 내부를 어떻게 적분할까?
지금까지 해온 방식과 정확히 동일하다.
3차원 내부를 n개의 직육면체로 분할하구 각 직육면체 위에 함숫값을 높이로서 곱한 4차원 부피를 구한뒤 이들을 더해나가면 된다.
이러한 방식을 삼중적분(Triplr Intergral)이라고 부르며 수식으로는
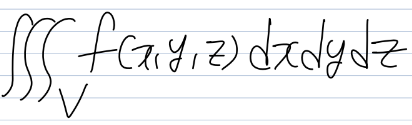
로 표기한다. 우리가 찾고자 하는 f(x,y,z)는 만족시켜야 하는 우변은

백터장F(F1,F2,F3)이 3차원 공간 V의 경계면인 S를 따라 나가는 양
직관적으로는 F가 경계면을 빠져나가는 양은 F가 내부에서 폭팔하는 양의 총량과 같다.
벡터의 폭팔은 바로 ▽·F이다. (현대물리학의 태동편 참고)
따라서 f(x,y,z)의 정체는 divergence가 되어야 한다.
발산 정리
폐곡면 S의 내부 영역을 V라 했을 떄 다음이 성립한다.

'Math > A journey to 근대 수학' 카테고리의 다른 글
| 17. 리만 복소해석학 (0) | 2022.08.21 |
|---|---|
| 16. 미분기하,위상수학 (0) | 2022.08.13 |
| 14-2) 다변수 미적분학 qna!! (0) | 2022.08.06 |
| 14. 다변수 미적분학 (중) (0) | 2022.08.02 |
| 13. 다변수 미적분학 (상) (0) | 2022.07.24 |




