나의 작은 valley
[딥러닝] 모델 학습법 본문
딥러닝 모델 학습법에 대해서 알아보자.
인공지능의 작동 원리.

입력값(x,y)을 특정 모델에 넣으면 예측값이 나온다. 이때 model에는 입력값에 가중치를 곱해주는 파라미터가 존재한다. 이후 예측값과 정답 값과의 오차를 loss function을 통해 구한다. loss 값을 기반으로 모델의 파라미터를 loss를 줄여주는 방향으로 업데이트한다.
인공뉴런

딥러닝은 인공 뉴런을 통해 학습을 한다. 그림은 입력 데이터를 model에 넣어주는 과정을 세분화한 그림이다. 입력된 값들에 가중치(파라미터의 일종)를 곱하고 bias(파라미터)를 더한 값을 activation_ function에 넣어준다. activation_function은 종류가 다양한데 여기선 WX + b의 값이 Theta보다 크면 1을 출력하고 작다면 0을 출력하는 함수이다.
ex) 실례를 통해 작동과정을 살펴보자.

x,y라는 입력 값에 각각 1이 곱해져서 들어온다. theta 값은 1이고 bias는 0이다. 그러면 output이 1인 경우와 0인 경우가 오른쪽 선을 기준으로 나뉘어진다. 즉 인공뉴런을 사용하면 선형 분리를 하는 것이 가능해진다.
MLP

Layer n에 있는 임의의 한 뉴런이 Layer n-1에 있는 모든 뉴런과 연결되어있는 구조를 MLP(Muti-Layer- Perceptron) 이라고 한다.
Activation Function
위에 인공뉴런을 설명할 때 입력 데이터에 가중치를 곱하고 bias를 더한 값을 바로 사용하는 것이 아니라 activation_function에 넣어준 것을 기억할 것이다. 그 이유는 해당 값 자체를 사용하면 선형한 상황을 피할 수 없기 떄문이다. 그러니깐 WX+b 그 자체를 output으로 보내면 그 다음 Layer에 입력값으로 WX+b가 입력값이 될 것이다. 그 Layer의 output은 다시 W(WX+b)+b 꼴이 될 것이다. 즉 선형한 상황 외로는 표현을 할 수가 없다. 따라서 activation func이 필요하고 sigmoid, ReLu, tanh 등 다양한 함수를 사용한다.
경사하강법

경사하강법은 최적화 알고리즘의 일종으로 사용된다. 처음 임의의 파라미터로 예측값을 구하고 결과값과 비교하여 loss를 구했을 때 어떻게 하면 loss를 줄이는 방향으로 파라미터를 업데이트할 수 있을까. 해당 점에서의 기울기들을 구한 다음에 반대 방향으로 파라미터를 업데이트 한다. 맨 밑의 식을 보면 되는데 기존 파라미터에 학습 속도를 의미하는 ir 변수 x 기울기 값을 빼주고 있다.
확률적 경사하강법

경사하강법의 문제점은 다음과 같다. 손실 함수에 극소값이 존재하면 더이상 업데이트가 되지 않는다. (기울기가 0이여서) 이러한 문제를 해결하기 위해 확률적 경사하강법이라는 기법이 탄생했다. 전체 데이터가 아닌 일부 데이터들을 돌아가며 사용하여 손실 함수를 만들어서 모델 구조를 변경해 극솟값을 없애는 것이다. 해당 방법에 또다른 이점은 전체 데이터를 사용하지 않아 계산량도 적어진다.
cf) 전체 M개의 데이터 중 m개를 골라 학습을 진행하는데 이떄 m을 batch라고 한다.
cf_2) M을 모두 학습한 횟수를 epoch이라고 한다.
sigmoid
활성화 함수로 sigmoid함수를 자주 사용하는데 이유는 다음과 같다. 경사하강법 수식을 보면 미분을 해주어야함을 확인할 수 있고 sigmoid 함수는 모든 지점에서 미분가능한 함수이기 때문이다.
역전파(back propagation)
∇f 라는게 모든 입력 값들에 대한 기울기를 원소로 가지는 matrix이다. 죽 ∇f를 구하기 위해서는 모든 파라미터들에 대한 미분이 필요하다. w,b를 구하는 과정은 SGD(확.경.하)로 가능하지만 모든 파라미터들에 대한 미분을 하는 것은 꽤 많은 연산량을 요구하는 일이다. 이 계산 과정을 간소화해주기 위해 등장한 방식이 역전파이다.
계산 그래프.

전체 편미분을 하기 위해서 작은 단위로 쪼개는 과정을 걷치는데 이때 계산 그래프를 사용한다.
Chain Rule

합성함수 미분을 하는데 쓰이는 테크닉이다. 속함수에 대한 미분을 진행하고 속함수 자체를 미분하는 식으로 합성 함수를 미분할 수 있다. 이때 chain 처럼 소거가 되는 방식이기에 chain rule이라고 한다.
Chain Rule를 적용하여 ∇f 구하기.

앞에서 구한 값을 기억해서 뒤에 위치한 Layer를 업데이트할 때 필요한 연산의 수를 줄여준다.
대표적인 역전파
- '+' 연산의 경우 역전파는 다음과 같이 전개된다.

즉 원래의 신호가 그냥 유지가 되며 전달된다.
- 'x' 연산의 경우 역전파는 다음과 같이 전개된다.

즉 다른 쪽의 edge 값이 곱해진 값이 전달된다.
EX)

이런 형태의 데이터가 존재한다고 가정하자. 그러면 f로 나오는 예측값은 -12이다. 실제 값은 -10이기 때문에 MSE를 사용하면 loss 값은 4가 된다.

각 파리미터를 업데이트하기 위해서는 각각을 Loss 함수에 대한 편미분을 진행해야 한다.

위에서 언급한 방식으로 각 파라미터의 기울기 값들을 모두 구했다. ir 값을 0.01로 두었을 때 parms - ir x 기울기 연산을 진행하면 업데이트된 파라미터들의 값은 다음과 같다.
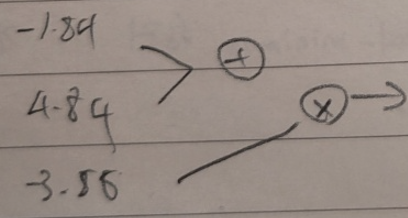
이후 다시 예측값을 구하면 -11.64라는 값이 나오는데 이는 이전의 예측값보다 더 정확한 예측값임을 확인할 수 있다.
역전파의 수학적 증명


이런 느낌으로 전달이 된다. +일 때는 output이 그대로 유지되고 x일 때는 인접한 가중치를 곱하고 넘어감을 확인할 수 있다. 좀더 직관을 발휘하면 활성화 함수의 미분값과 활성화 함수 값 그 자체가 가중치 변화에 따른 비용 함수 변화에 영향을 주는 것을 확인할 수 있다.
즉 미분값이 0에 가까울 경우, 가령 sigmoid 함수에서 y값이 1또는 0에 가까운 경우 가중치의 변화가 손실 함수에 주는 영향이 낮음을 알 수 있다.
손실 함수
마지막으로 어떤 손실 함수를 사용하는 것이 유리한지에 대한 이야기를 하고 글을 마치겠다.
-역전파 관점

아래의 그래프는 sigmoid 함수의 도함수이다. 양 끝쪽으로 갈수록 값이 낮아짐을 확인할 수 있다. 즉 초기 파라미터의 값이 무엇이냐에 따라 학습 속도에 영향을 준다.

cross entropy의 경우 Error가 a_f의 영향을 받지 않기 떄문에 역전파의 관점에서는 cross entropy를 사용하는 것이 학습에 유용하다.
cf) 아니면 모든 지점에서 미분 값이 똑같은 함수를 쓰던가.(LeLU)
-Maxximum Likelihood의 관점
데이터가 확률 함수의 꼴을 가지는 경우 가장 높은 확률을 나오는 지점을 예측값으로 해서 확률 함수 자체를 이동시키는 방식.
-> 결론만 쓰면 데이터의 분포가 가우시안 분포이면 MSE를 사용하고 베르누이 분포면 cross-entropy를 사용한다.
진짜 마지막) what is cross entropy

https://www.youtube.com/watch?v=34R_5FumoGw
마치며
인공뉴런의 개념을 이해하고 각 부분들의 작동 방식 등등을 알아보는 시간을 가져보았다.
'Computer Science > [인공지능]' 카테고리의 다른 글
| [딥러닝] Tensor Manipulation (2) | 2024.03.15 |
|---|---|
| [딥러닝] 성능 고도화 (0) | 2024.03.12 |
| [Ai] 클러스터링 (0) | 2024.02.20 |
| [AI] 분류 (0) | 2024.02.08 |
| [AI] 회귀 (0) | 2024.02.06 |




